Maths


Capacitance


In the examples we are using the CASIO fx-83MS calculator ( unless other wise stated ) if you are using another calculator refer to the user manual for any differences.

In this section we come across the formula

Remember we are dealing here with Capacitors in parallel and capacitors in series.


Example What is the total capacitance in microfarads for C1 = 3uF C2 = 5uF C3 = 10uF ?

Capacitors in parallel have their values added together.

3 5 10 Result 18

If you had been asked to give the answer in nano farads which is 1/1000 or 10-3 smaller then you would press the key until you see -03 Result 18000 nanofarads
You must know which exponential you are looking for with the key otherwise you can still end up with the wrong answer.
This is the formulae for two capacitors in series.

Example What is the total capacitance in microfarads for C1 = 3uF C2 = 5uF ?

3535
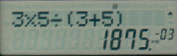If you had been asked to give the answer in nano farads which is 1/1000 or 10-3 smaller then you would press until you see -03 and the Result 1875 nanofarads
This is the formulae for more than two capacitors in series.

Example What is the total capacitance in nanofarads for C1 = 3uF C2 = 5uF C3 = 10 C4 = 28 ?

131110 128 Result 0.669uF when we round to 3 places of decimal.

but this is so one last function press which give the reciprocal.

then for the final result, well nearly !!!!

BUT you had been asked to give the answer in nano farads which is 1/1000 or 10-3 smaller so you need to press until you see -03 and the Result 1494 nanofarads if we forget the figures after the decimal point. In an exam it would be expected that when asked for nanofarads then it wold be a whole number !!
Again this example invokes the "Maths rule" with the division being done first before the addition so no brackets are required.
In this last example the full screen of figures is shown as on the calculator and has not been widened, as by now you should be familiar with what to expect in the display. From now on we leave out the button as you know how to use it!

T=CR

 T (in seconds) = C (in farads) x R ( in ohms)
Here as with ALL formula the value of the variables must be considered. It is not often that you will use a capacitor as large as a Farad the microfarad uF being more usual.
Example . How long in seconds will it take for a 470uF capacitor to charge to 63% of the applied voltage VS 5V through a resistor of 1k2

In this example we are using the

In this example because we are using a "wrong" mix of numbers, by that we have components which are not in the prefix correct for the equation we will have to enter the number expressing them in terms of the prefix we need.

To do this we need to introduce you to the exponential key . we know that 470uf can be written as 470 x 10-6 Farads and 120kΩ can be written as 120000 or 120 x 103Ω so we will be using this in the calculator input. So back to the question.

How long in seconds will it take for a 470uF capacitor to charge to 63% of the applied voltage VS 5V through a resistor of 120kΩ

470 6 120 3
Result 56.4 seconds
So by expressing the values given to those required by the formula the answer comes out directly!! 

So that completes the calculations for this set and it is hoped that by now the benefit of the use of the calculator is showing through the blur of figures.

There are more functions to show you but it is hoped that you have taken all the above onboard and it is time to give yourself a coffee / tea break !!!

Next Inductance



First page of Advanced course

First page of site