

Understand the equations for decibel power and voltage ratios.
The equations are :-
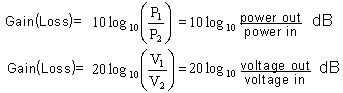
When assessing the sound level strength of an audio signal this is how loud it seems to be when heard by the human ear. If someone thinks that a sound level has doubled when power from a audio amplifier is raised from 5 to 10 watts that same person should also consider that a signal would also be twice as loud if the power increased from 200 to 400 watts. The human ear has what is called a "logarithmic" response to changes in audio levels. It is this basis that is used for the "relative" power level given the name of "the decibel" (dB). One decibel is 1/10th of a bel the unit of sound coined by Alexandra Graham Bell.
The number of decibels in relation to the ratio of power levels is given by :-
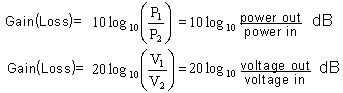
When using the V1 / V2 voltage equation the the impedance must be the same for both voltages, thus a power amplifier cannot be properly assessed if only taken on input and output voltages, unless those voltage have the same value of impedance in the circuit.
These equations look very complex but in the scientific calculator sections it is shown how the equations can be used when P1 = PowerOut, P2 = PowerIn, similarly V1 = VoltsOut and V2 = VoltsIn
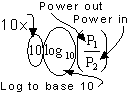
The log to the base 10 is the usual log used by engineers and would be that on the scientific calculator. The 10 in front of "log" means multiply the log of the ratio P1/P2 by 10, the resulting answer will be the relative power expressed in dBW or decibel watts.
![]()
When the decibel value (dB) and one power value is known then the unknown power can be calculated from the equation at the left.
We are using log to the base 10 as shown by "log10" the 10 to the right of the word log indicate base 10. For clarity we will now omit that 10 and only write "log".
in is not shown then assume that it is 1 Watt.
Example: What is a measured power of 400W expressed in dBW ?
dBW = 10 log(power in watts)
dBW = 10 log(400) = 26dBW Click here to see the calculator key strokes
Example: What is a measured power of 12dBW expressed in Watts ?
Power(Watts) = antilog dBW/10
Power(Watts) = antilog 12/10 16 Watts Click here to see the calculator key strokes
There is another equation that is given in the equation listing.
![]()
This is used to determine the gain of a yagi over a dipole using the power from each.
Revision: Recall (or determine) the power gain or loss of various dB ratios based on ± 3, 6, 9, 12, 15 and 10, 20, 30dB.
Power gain - always a + but often assumed, with no plus sign.
| dB | Calculation | Gain (Rounded figures) |
| +3 | antilog 3/10 | x 2 |
| +6 | antilog 6/10 | x 4 |
| +9 | antilog 9/10 | x 7.94 |
| +10 | antilog 10/10 | x 10 |
| +12 | antilog 12/10 | x 15.8 |
| +15 | antilog 15/10 | x 31.6 |
| +20 | antilog 20/10 | x 100 |
| +30 | antilog 30/10 | x 1000 |
Power loss, always a minus sign in front of the dB number.
| dB | Calculation | Loss (Rounded figures) |
| -3 | antilog 3/10 | ÷ 2 |
| -6 | antilog 6/10 | ÷ 4 |
| -9 | antilog 9/10 | ÷ 7.94 |
| -10 | antilog 3/10 | ÷ 10 |
| -12 | antilog 12/10 | ÷ 15.8 |
| -15 | antilog 15/10 | ÷ 31.6 |
| -20 | antilog 20/10 | ÷ 100 |
| -30 | antilog 30/10 | ÷ 1000 |
The origin of some of the text on this page is from the RSGB with additions by the web master