|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
Syllabus Sections:- Transformers 2G1 14 Understand the concept of mutual inductance. If two coils with their axes aligned on the same line then the current passing though one of the coils creates a magnetic field around itself and also around the second coil which has the mutual effect of INDUCING an EMF in this second coil. However the current passing in the first coil only induces an EMF in the second coil when the field strength of the magnetic field is changing and this is from and AC source only. Thus the MUTUAL EFFECT of the magnetic field passing around both coils results in MUTUAL INDUCTANCE and causes the EMF in the second coil. When all the magnetic field, or magnetic flux as it is sometimes called set up by the fist coil cuts all the turns of wire in the second coil the mutual inductance reaches its maximum possible amount. The amount of coupling is related to the distance between the coils. If the coils are some distance apart then the coils are said to be loosely coupled. The maximum coupling is achieved when the two coils are wound one on top of the other. The minimum coupling is when they are placed far apart or at right angles to each other.
2G1
14 continued Understand and
apply the formula relating transformer primary and
secondary turns to primary and secondary potential
differences and currents. Maths formula also most
certain to be used in this question !!! The formulae are
:- Here we are dealing with AC as we are considering transformers! Transformers and potential differences In the formulae :- Vp = Volts in the primary coil (or the driven coil) Vs = Volts in the secondary coil Np = Number of turns in the primary coil Ns = Number of turns in the secondary coil Ip = current passing in the primary coil Is = Current passing in the secondary coil Re-arranging
the formula the ratio
of the input turns This is a simple comparison of input and output. From the above it is possible to calculate the transformation of voltage from the primary to the secondary such as you would need to do if building a power supply. Example: A transformer has 200 turns on the primary and 100 on the secondary and an input voltage of 50 volts. What is the calculated output voltage ? applying the figures to the formula Vs = 50 x 100/200 answer 25 volts. Transformers and currents Re-arranging
the formula the ratio
of the output turns This is not quite so straight forward but is based on the Power equation P = V x I. Thus what
is put in as power one side (Vin x In),
assuming no losses will come out as power the other (Vout
x Iout). This
leads to the equation The
equation says that the current in the primary Putting some figures to this if there is 240 volts on the primary of 100 turns and 24 volts at 10 amps on the secondary - there would be less current at 240 Volts in the primary. With this in mind let's work it out. From the
equation From the
equation so Ip / 10 = 10 / 100 thus Ip = 10 x 10 / 100 answer 1 amp If you were given the current that can be supplied from the primary you can find out what current can be taken from the secondary such as you would need to do if building a power supply if you know the turns ratio. So now
using this formula Example: A transformer can allow a secondary coil current of a maximum of 20 amps and it has 400 turns on the primary and 100 on the secondary what is the required input current capability ? Applying the figures to the formula Ip = 20 x 100 / 400 answer 5 amps.
2G1 14 Understand the impedance change in a transformer and apply formula relating transformer primary and secondary turns to primary and secondary impedances. The formula is :- Matching input and output impedances In a perfect situation -one without reactance losses or leakages the above equation would hold true where:-
The primary terminal impedance is determined by the equation being dependent only upon the load resistance and the turns ratio. Where would this be used? Say a AF amplifier required a load of 200ohms to operate properly and you are driving an 8ohm speaker then you could, assuming a perfect world, design an impedance transformer to ensure the criteria was met.
|
|||||||||||||
|
|
|||||||||||||
|
|
|||||||||||||



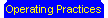



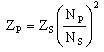
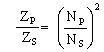 by taking the
square root of both sides
we get
by taking the
square root of both sides
we get 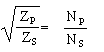 =
= 