Syllabus Sections:-

Power

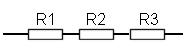
Resistors

Resistors and what they are was introduced to you in the Foundation Licence course and developed in the Intermediate Licence course.

There are two quite different and for some of you reading the course challenging formulae associated with resistor combinations whether they are in series or in parallel

Resistors in Series

The diagram below shows resistors connected in series.

For a calculation any number of resistors, (from as few as two) may be connected as shown above.

The effective resistance of the combination of R1 R2 and R3 is given by

R(total) = R1 + R2 + R3

BUT you can of course add together as many resistors as you need to and calculate the total effective resistance of all the resistors.

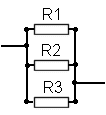
Resistors in Parallel

The diagram below shows resistors connected in parallel.

Note that all the resistors are linked to each other by the wire that is across the end of of them all so it does not matter where the other wires connect to the circuit the result would be the same.

For a calculation any number of resistors, (from as few as two) may also be connected as shown above.

The effective resistance of the combination of R1 R2 and R3 is given by

which can also be written as :- 1/R(total)= 1/R1 + 1/R2 + 1/R3

BUT as with the earlier example you can of course add together as many resistors as you need to and calculate the total effective resistance of all the resistors.

Let's put in some values. R1 = 100 ohms R2 = 150ohms R3 =270ohms

Thus 1/R(total) = 1/100 + 1/150 + 1/270

so 1/R(total) = 0.01 + 0.0066 + 0.0037

so 1/R(total) = 0.0203

so R(total) = 1/0.0203

so R(total) = 49.26

So the total resistance of R1, R2 and R3 in parallel is about 49 ohms

Note:- that the resulting resistance is always less than the lowest resistor value in the group.

However consider what would happen in a mix of series and parallel..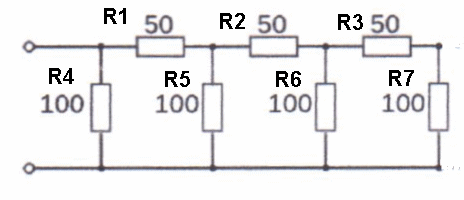


Looking at R3 and R7 they are linked in Series so total value is 150 Ω call that R8
Now look at R2 and R6 they too are link in Series

they are linked in Series so total value is 150 Ω call that R10

So now we have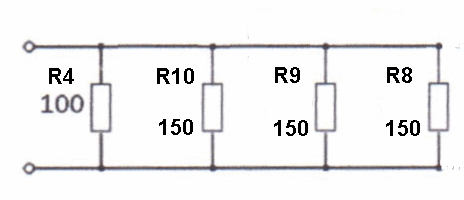

We now have R4 R10 R9 and R8  in parallel

So 1 / Rtotal = 1 /100 + 1 /150 + 1/ 150 + 1/ 150

Thus 1 / RTotal = (150+ 100 + 100 +100) / 15000
                         =   450 / 15000
                          = 0.03
thus RTotal =  33 Ω

For the exam do the calculation as shown and then compare you answer to that in the question and you will see what figure is like yours and pick that as the correct answer.

If you are weak on maths then ask your lead instructor for some extra work on this to help you learn it.