|
|
|||||||||||||||||
|
|
|
||||||||||||||||
|
|
|||||||||||||||||
|
Syllabus Sections:- A.C. circuits Part 2 2E3 12 Recall that current lags potential difference by 90° in an inductor and that current leads by 90° in a capacitor. Re-writing the syllabus makes it easier to understand Recall that potential difference leads current by 90°in an inductor and that current leads potential difference by 90° in a capacitor.
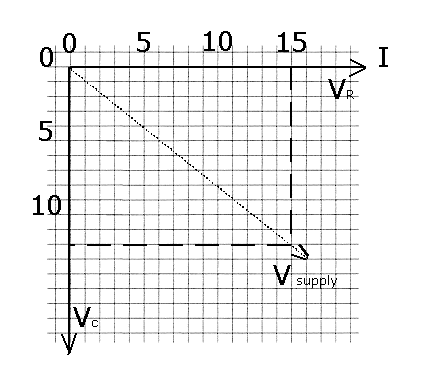
However the voltage across the capacitor will lag the current by 900 and the voltage can be determined by V = I x Xc So you cannot just add the voltages but they have to be added using a vector diagram.
Memory aid: This section is quite difficult to grasp for some students so an old hand at Amateur Radio, at a recent BRATS club meeting, suggested the following was added to the course notes. C I V I LC I V......V I Lwith a Capacitor the current leads the voltage the so I leads the V thus this gives us Capacitor IV and with an Inductor voltage leads the current so V leads the I thus this gives VI L (Inductor) With that in mine continue with the topic.
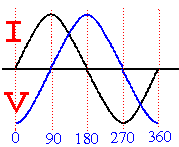
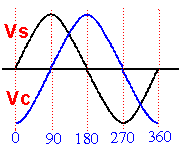
Capacitor - Current leads Potential Difference (C I V ) If the black curve now represents the current through a capacitor then the blue curve represents the potential difference across a capacitor. The current leads the potential difference by 900. This capacitive reactance can be
calculated by the formula XC=
1/2 f is in Hertz with C in Farads Inductor - Potential difference leads the Current ( V I L ) If the black curve represents the potential difference across an inductor then the blue curve represents the current across an inductor. The potential difference leads the current by 900. So let us explain further. When the Black curve is at position 0 the blue curve has not yet reached the same 0 position thus the black cure is said to lead the blue curve. This inductive reactance can be calculated
by the formula XL=2 f is in Hertz with L in Henrys PD (voltage Wave forms) Taking this further at the point of supply of AC the wave forms of PD potential difference (voltage) and Current are in phase but when it encounters a capacitor then from above the current leads the PD (voltage) CIV thus in fact across the capacitor the PD or voltage wave will lag behind the supply waveform. Had it been an Inductor then the PD (voltage) leads the current VIL thus in fact across the Inductor the PD or voltage wave will lead the supply waveform. Can you draw the appropriate wave forms ??
Recall that the term 'reactance' describes the opposition to current flow in a purely inductive or capacitive circuit where the phase difference between V and I is 90°. 2E3 12 Understand the formulae for the reactance of a capacitor or inductor in terms of frequency and component value. Calculate the unknown term given the other two. The
equations are :- Reactance Reactance is the opposition to current flow in an AC circuit and can be loosely thought of as AC resistance and has values in ohms. This "AC resistance" is not actually resistance and it must be remembered that a capacitor stores energy electrostatically and an inductor stores energy magnetically. Taking the case of the capacitor it can be loosely thought of as a very small rechargeable battery which accepts a charge and can then accept no more. On the next half cycle the capacitor then gives up that charge back to the supply and charges in the opposite direction. For this reason a "perfect capacitor" (one with no losses) does not get hot. It will be appreciated that the capacitor will charge and once charged can pass no more electricity hence it then apparently acts as an open circuit. To differentiate from "normal" resistance we call that caused by the capacitor Capacitance Reactance and that by an inductor Inductive Reactance and both have values in ohms. In the formulae that follow they use certain symbols :-
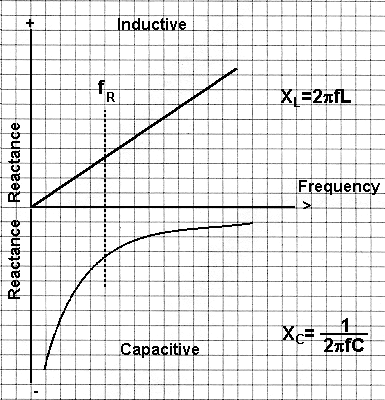
Inductive Reactance If we
draw a graph of inductive reactance
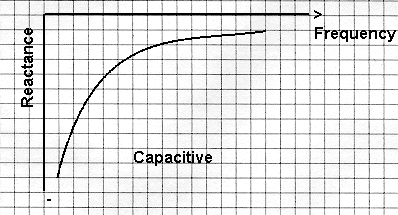
Capacitive Reactance If we
draw a similar graph for capacitive reactance
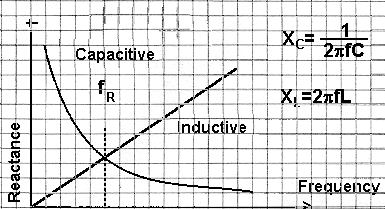
Resonance Now, if we have an LC circuit and draw both graphs on a common frequency line we get :-
Series Resonance We have
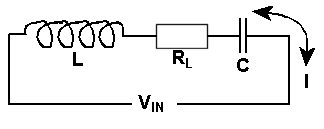
spoken about the reactance of the coil (inductor) which is
like resistance but the coil still has "normal" resistance and
for these calculations we call this Let as Thus Thus Voltage
across Thus
Voltage across Thus
Voltage across Gain The "gain" between the input and the output is known as magnification factor which in this case = 1000 (10mV rising to 10V = 1000 times) and thus the magnification
factor at resonance =
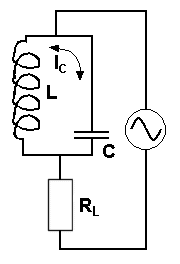
Parallel Resonance
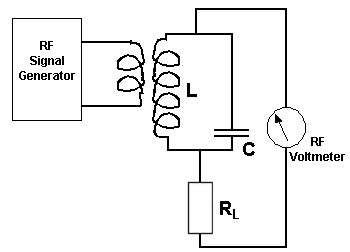
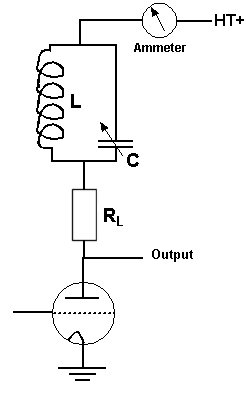
Resonance CurvesAssuming that we loosely couple a signal generator into the inductor of a parallel LC circuit and measure the voltage across with an RF voltmeter
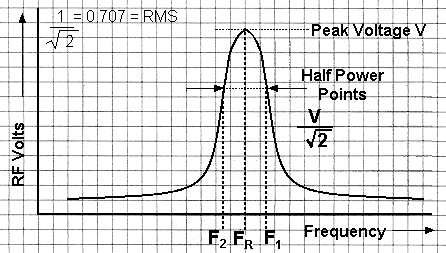
The
points either side are generally accepted as limits of usable
frequency - This range Q Meter This measurement, requiring only a voltmeter, is used in a common form of Q meter. Q meters give a measure of "Goodness" of a component or circuit. In this case ie the Bandwidth compared to the resonant frequency = SELECTIVITY In the
exam the sheet of equations shows this formula as fC = centre frequency fU = the upper frequency and fL = the lower frequency
There is also something called Carson's rule which is related to the above This defines the approximate modulation bandwidth required for a carrier signal that is frequency-modulated by a spectrum of frequencies rather than a single frequency. The Carson bandwidth rule is expressed by the relation Bw = 2(Af+Δf ) Where Bw is the bandwidth requirement, Af is the highest modulating frequency Δf is the carrier peak deviation frequency For example, Carson's rule would say that the bandwidth or speech (300Hz to 3kHz) with a peak deviation of 5kHz would be. Bw = 2(3kHz+5kHz) Bw =2*8kHz Bw =16kHz
Longwave Coils (for interest only)If we build a receiver for say 120kHz, the RF stage (if we still require 12kHz speech bandwidth) will have a measured "MAX" NOTE: a Providing The parallel resistance
of a tuned circuit at resonance is
The general expression for Dynamic Resistance is :- It is obvious from this
that the larger
2E4 12 Understand the use of capacitors for AC coupling (DC blocking) and decoupling AC signals (including RF bypass) to ground. It should be clear to you that from the construction of a capacitor (two separate plates with no link between them) provided no path for DC to pass. Thus it can be said that capacitors block DC and thus can be used for blocking DC in a circuit. On the other hand in an AC circuit current appears to pass because of the build up and decay of the charge on one plate and then the other AC changes direction of its flow of electrons. If therefore there is the possibility of an AC signal (and this include RF which is also AC) in a DC circuit then this can be channelled to ground via a capacitor and as such this is called decoupling hence the term "decoupling capacitor". Take
a look at --------------------------------------------------------------------------------------------------------------- 2E5 12 Understand the use of inductors for DC decoupling (AC blocking) An inductor is a passive electronic component which is capable of storing electrical energy in the form of magnetic energy. Basically, it uses a conductor that is wound into a coil, and when electricity flows into the coil it will generate a magnetic field. If we assume that an AC is flowing through the inductor. When current is about to flow to the inductor, the magnetic field generated by that current cuts across the other windings, giving rise to an induced voltage and thus preventing any changes in the current level. These effects of the induced voltage
are produced even when the direction in which the current
is flowing is reversed. Before overcoming the induced
voltage that is attempting to block the current, the
direction of the current is reversed so that there is no
flow of current.
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||
|
|
|||||||||||||||||







 fC
fC 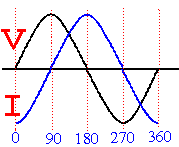

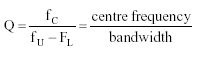
 page 35 Fig 5.19 and C3 is acting as
a "decoupling capacitor" as the circuit is amplifying AC
signals but any that might flow from the emitter of the
transistor will be taken to ground via the Capacitor C3 but
any DC signal will not be passed in stead it will travel to
ground through R4.
page 35 Fig 5.19 and C3 is acting as
a "decoupling capacitor" as the circuit is amplifying AC
signals but any that might flow from the emitter of the
transistor will be taken to ground via the Capacitor C3 but
any DC signal will not be passed in stead it will travel to
ground through R4.
