

2F1 Understand that analogue to digital conversion can generate a false image of the signal if frequencies are present above the frequency which is half the sampling (Nyquist) rate
In electronics, an analog-to-digital converter (which can be abbreviated to ADC, A/D, or A-to-D) is a system which converts an analog signal, such as a sound picked up by a microphone into a digital signal. It must take a sample of the input signal at least 2x as quick as the highest frequency to be used is it can reproduce the original signal in the digital format wanted, if not done this way aliases (false images ) are produced. The minimum required sampling rate (2 x) is known as the Nyquist rate after Harry Nyquist an electronic engineer.
When performing analog-to-digital conversion (ADC), the process involves sampling the continuous-time analog signal at discrete intervals and converting these samples into digital values. If there are frequencies in the signal that are higher than half the sampling rate (also known as the Nyquist rate), aliasing can occur, leading to a false or incorrect representation of the signal in the digital domain. Here's how that happens:
Nyquist Rate and Sampling Theorem
The Nyquist-Shannon Sampling Theorem states that to accurately reconstruct an analog signal, it must be sampled at a rate at least twice the highest frequency present in the signal. This means:
fs = 2fmax
You do not have to remember this for the exam, it is here for clarity.
Where:
fs is the sampling rate (samples per second)
fmax is the maximum frequency of the signal (highest frequency component).
The critical point is that if the signal contains frequency components above fs / 2, those higher frequencies cannot be represented correctly by the discrete samples.
Recall that these false images are know as aliases
Aliasing
When the sampling rate is not high enough (i.e., if the signal contains frequency components above half the sampling rate), aliasing occurs. This means that higher frequency components of the signal get mapped (folded) back into lower frequencies, causing distortion.
Aliasing is a phenomenon where high-frequency components (those above fs /2) are misrepresented in the sampled data. They get incorrectly mapped to lower frequencies, producing a "false" image of the signal. This distortion cannot be corrected after the sampling process.
For example, if you sample at a rate of 8 kHz (so the Nyquist frequency is 4 kHz), any frequency component above 4 kHz will appear as a lower frequency in the sampled data, and the original signal will be misrepresented.
How Aliasing Works
When the sampling rate is not high enough (i.e., if the signal contains frequency components above half the sampling rate), aliasing occurs. This means that higher frequency components of the signal get mapped (folded) back into lower frequencies, causing distortion.
Suppose there is a component in the original signal at a frequency fs = 6 kHz, which is above the Nyquist frequency. According to the sampling theorem, the signal cannot be correctly sampled because the Nyquist rate (4 kHz) is less than the signal frequency (6 kHz). In this case, the 6 kHz signal will "fold" over into the lower frequencies. Specifically, it will appear as a frequency of (6 kHz-4 kHz) = 2 kHz in the sampled data.
So, instead of capturing the 6 kHz component accurately, the ADC will produce a false representation where it looks like a 2 kHz signal. This is aliasing, and it distorts the representation of the original signal.
Understand that anti-aliasing filters are used to avoid this occurring,
Preventing Aliasing
To avoid aliasing and ensure accurate digital representation of the analog signal, one of the following must be done:
Increase the Sampling Rate: The sampling rate must be sufficiently high to satisfy the Nyquist condition. For instance, if the highest frequency in the signal is 10 kHz, the sampling rate must be at least 20 kHz.
Use an Anti-Aliasing Filter: Before sampling, an anti-aliasing filter (a low-pass filter) is often used to remove frequency components above the Nyquist frequency, ensuring that the signal only contains frequencies that can be accurately sampled.
Summary of the Process
To avoid aliasing: Either increase the sampling rate or apply an anti-aliasing filter to limit the signal’s frequency content. If the sampling rate is too low: Frequencies above half the sampling rate will be incorrectly represented.
Aliasing occurs when these high frequencies fold back into the lower frequency range, creating a distorted or false image of the signal.
Example:
Let's assume an analog signal has two frequency components:
f1 = 2 kHz (which is below the Nyquist rate for a 5 kHz sampling rate),
f2 = 6 kHz (which is above the Nyquist rate for a 5 kHz sampling rate).
If we sample at 5 kHz:
The 2 kHz component will be sampled correctly.
The 6 kHz component will alias to (6-5) =1 kHz, causing it to be misrepresented as 1 kHz instead of 6 kHz.
Thus, the signal reconstructed from the samples will incorrectly show a 1 kHz frequency component instead of the original 6 kHz component, leading to a false representation of the signal.
This highlights the importance of sampling at a rate high enough to accurately capture the frequency content of the analog signal without introducing aliasing.
2F2 Recall that digital signals in this time domain can be depicted in the frequency domain by using a mathematical operation known as a Fourier Transform (FT)
Digital signals in the time domain can be depicted in the frequency domain through the Fourier Transform (FT). The Fourier Transform is a mathematical operation that decomposes a time-domain signal into its constituent frequencies, providing a frequency-domain representation of the signal. The general idea is to express a signal as a sum of sinusoidal components, each with a specific frequency, amplitude, and phase.
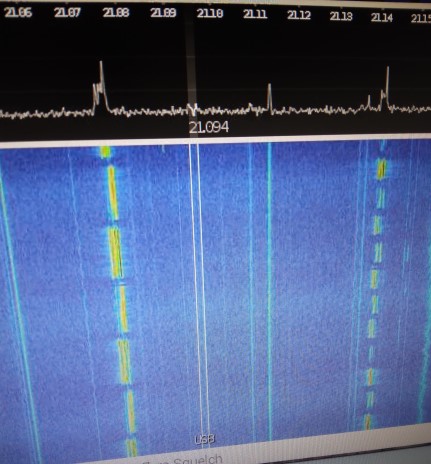
Fourier Transform (FT) Overview:
Given a continuous-time signal x(t), the Fourier Transform X(f) converts this time-domain signal into a frequency-domain representation.
A Time-Domain graph shows how a signal changes over time (this is the usual one depicted on an oscilloscope, with amplitude in the y axis and time on the x horizontal axis), whereas a frequency-domain graph shows how much of the signal lies within each given frequency band over a range of frequencies.
Recall that a Fourier Transform takes digital signals in the time domain and calculates the amplitude and the frequencies which comprised the original signal.
When an analogue signal is sampled it has an amplitude data stream that can be transformed (via a mathematical process called the Fourier Transform ) into a different set of data that shows the amplitude signals present in the frequency order of the sample.
Fast Fourier Transform (FFT):
The FFT is an efficient algorithm for computing the DFT, which is particularly useful for long signals or large datasets.
Steps for Fourier Transform in Time to Frequency Domain:
Signal Representation: Start with the time-domain signal (either continuous or discrete).
Apply Fourier Transform: Apply the Fourier Transform (or DFT for digital signals) to convert the signal from the time domain to the frequency domain.
Interpret Frequency Spectrum: Analyze the frequency spectrum obtained. The result will show how much of each frequency is present in the signal, and how the signal is composed of different frequency components.
Example:
For a discrete-time signal like a sampled sine wave, applying the DFT would give a spike at the frequency corresponding to the sine wave. The magnitude at that frequency would indicate the amplitude of the sine wave, and the phase would give information about the signal's phase shift.
In conclusion, the Fourier Transform (or DFT) transforms the time-domain representation of a digital signal into its frequency-domain representation, revealing the signal’s frequency content.
The origin of some of the text on this page is from the RSGB with additions by the web master