

2G1 Understand the concept of mutual inductance
If two coils with their axes aligned on the same line then the current passing though one of the coils creates a magnetic field around itself and also around the second coil which has the mutual effect of INDUCING an EMF in this second coil.
However the current passing in the first coil only induces an EMF in the second coil when the field strength of the magnetic field is changing and this is from an AC source only.
Thus the MUTUAL EFFECT of the magnetic field passing around both coils results in MUTUAL INDUCTANCE and causes the EMF in the second coil.
When all the magnetic field, or magnetic flux as it is sometimes called set up by the fist coil cuts all the turns of wire in the second coil the mutual inductance reaches its maximum possible amount.
The amount of coupling is related to the distance between the coils. If the coils are some distance apart then the coils are said to be loosely coupled. The maximum coupling is achieved when the two coils are wound one on top of the other. The minimum coupling is when they are placed far apart or at right angles to each other.
2G1 continued Understand and apply the formula relating transformer primary and secondary turns to primary and secondary potential differences and currents.
Maths formula also most certain to be used in this question !!!
The formulae are :-
![]()
![]()
Here we are dealing with AC as we are considering transformers!
Transformers and potential differences
In the formulae :-
Vp = Volts in the primary coil (or the driven coil)
Vs = Volts in the secondary coil
Np = Number of turns in the primary coil
Ns = Number of turns in the secondary coil
Ip = current passing in the primary coil
Is = Current passing in the secondary coil
Re-arranging the formula:
![]() to
to ![]()
it is a little easier to see that the ratio of the
input voltage ![]() output voltage it equal to the ratio
of the input turns
output voltage it equal to the ratio
of the input turns ![]() divided by the output turns.
divided by the output turns.
This is a simple comparison of input and output.
From the above it is possible to calculate the transformation of voltage from the primary to the secondary such as you would need to do if building a power supply.
![]() the part Ns / Np is called the turns ratio and was
introduced to you in the Intermediate
Licence course click to check back.
the part Ns / Np is called the turns ratio and was
introduced to you in the Intermediate
Licence course click to check back.
Example:
A transformer has 200 turns on the primary and 100 on the secondary and an input voltage of 50 volts A.C. What is the calculated output voltage ?
Applying the figures to the formula Vs = 50 x 100/200
answer 25 volts.
Transformers and Currents
Re-arranging the formula ![]() to
to ![]() it is a little easier to see that the ratio of the
input current
it is a little easier to see that the ratio of the
input current ![]() output current is equal to the ratio
of the output turns
output current is equal to the ratio
of the output turns ![]() divided by the input turns.
divided by the input turns.
This is not quite so straight forward but is based on the Power equation P = V x I.
Thus what is put in as power one side (Vin x In),
assuming no losses will come out as power the other (Vout
x Iout). This leads to the equation ![]()
The equation says that the current in the primary ![]() the current in the secondary is dependent
upon ratio of secondary turns
the current in the secondary is dependent
upon ratio of secondary turns ![]() primary turns.
primary turns.
Putting some figures to this if there is 240 volts on the primary of 100 turns and 24 volts at 10 amps on the secondary - there would be less current at 240 Volts in the primary.
With this in mind let's work it out.
From the equation ![]() then 24 / 240 = Ns / 100
then 24 / 240 = Ns / 100
From the equation ![]() then Ns = 24 x 100 /240 answer = 10
turns Ns
then Ns = 24 x 100 /240 answer = 10
turns Ns
so Ip / 10 = 10 / 100
thus Ip = 10 x 10 / 100 answer 1 amp
If you were given the current that can be supplied from the primary you can find out what current can be taken from the secondary such as you would need to do if building a power supply if you know the turns ratio.
So now using this formula ![]()
Example:
A transformer can allow a secondary coil current of a maximum of 20 amps and it has 400 turns on the primary and 100 on the secondary what is the required input current capability ?
Applying the figures to the formula Ip = 20 x 100 / 400
answer 5 amps.
2G1 Understand the impedance change in a transformer and apply formula relating transformer primary and secondary turns to primary and secondary impedances.
The formula is :-
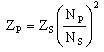
Matching input and output impedances
In a perfect situation -one without reactance losses or leakages the above equation would hold true where:-
The primary terminal impedance is determined by the equation being dependent only upon the load resistance and the turns ratio.
Where would this be used?
Say an AF amplifier required a load of 200 ohms to operate properly and you are driving an 8 ohm speaker then you could, assuming a perfect world, design an impedance transformer to ensure the criteria was met.
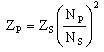 by
dividing both side by Zs we get
by
dividing both side by Zs we get
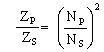 by
taking the square root of both sides we get
by
taking the square root of both sides we get
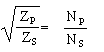 =
= ![]() = 5
= 5
So the primary turns must be 5 times as many as the secondary.
This impedance matching means altering the "load" impedance by the transformer to the required output level.
Not in the Full 2024 syllabus but used here for Information:
Understand the cause and effects of eddy currents and the need for laminations (or ferrites) in transformers.
Eddy Currents
When an AC supply passes through a coil, a magnetic field is generated. The size or density of the magnetic field can be increased by the use of an iron core such as is used in transformers. Iron being a conductor, the magnetic field causes an electric current to flow in the core. The current flow is called "EDDY CURRENTS".
Effect of the eddy currents
The effect of the eddy currents is a loss of power, as flowing through the resistance of the core they create heat. As you are aware from the Foundation Course if there is not a complete circuit a current could not flow.
Use of Laminations
So what can be done to stop the eddy currents in the iron core of the coil?
The solution is to make the core of thin strips of insulated iron material called "laminations" and for the lamination not to form a continuous loop around the coil. So a break in the lamination is formed and this small air gap is the necessary break in the circuit and the eddy currents cannot now flow.
Recall that different magnetic materials used as cores for inductors and transformers perform best over different frequency ranges and affect their efficiency.
Magnetic materials used as cores for inductors and transformers significantly affect their performance, especially in terms of efficiency, over different frequency ranges. The core material dictates how well the device performs under various operating conditions, including factors such as power losses, inductance, and overall energy efficiency. Here's how different magnetic materials perform across different frequency ranges and their impact on efficiency:
Types of Magnetic Materials Used in Cores
1. Soft Ferrites
Material Characteristics:
Soft ferrites are ceramic compounds composed of iron oxide combined with other metals like manganese, zinc, or nickel. They are typically used for high-frequency applications (from tens of kHz to several MHz).
Performance at Different Frequencies:
Low Frequencies:
At lower frequencies (up to a few kHz), ferrites are less efficient because their permeability decreases and they exhibit higher core losses. However, for frequencies above 10 kHz, their performance improves significantly.
High Frequencies:
Ferrites are excellent for high-frequency applications (hundreds of kHz to MHz). They offer low core losses, high permeability, and relatively low eddy current losses, making them ideal for radio-frequency (RF) applications and high-speed switching power supplies.
Efficiency:
Ferrites provide high efficiency at high frequencies due to their low eddy current losses, but at lower frequencies, they can cause higher core losses (hysteresis and eddy currents), reducing efficiency.
2. Iron Cores (Laminate or Solid)
Material Characteristics:
Iron cores, often in the form of laminated sheets to reduce eddy current losses, are commonly used in transformers and inductors for power applications. These are effective in low-frequency applications, particularly for mains frequency (50/60 Hz).
Performance at Different Frequencies:
Low Frequencies:
Iron cores are very efficient at low frequencies, especially for power transformers operating at 50/60 Hz. The lamination reduces eddy current losses, making them suitable for energy-efficient applications at low frequencies.
High Frequencies: At high frequencies (tens to hundreds of kHz and above), iron cores suffer from significant eddy current losses due to their high electrical conductivity. As a result, they become less efficient for high-frequency applications.
Efficiency:
Iron cores are highly efficient for low-frequency power applications but suffer from high core losses at higher frequencies due to increased eddy currents and hysteresis.
3. Amorphous Steel
Material Characteristics:
Amorphous steel (also known as "metallic glass") has a non-crystalline structure, which gives it better magnetic properties compared to conventional iron-based materials.
Performance at Different Frequencies:
Low Frequencies:
Amorphous steel performs well at low frequencies due to its very low core losses (both hysteresis and eddy current losses). It is often used in transformers that need to operate at or near the power line frequency (50/60 Hz).
High Frequencies:
Its performance at high frequencies (hundreds of kHz to MHz) is not as good as ferrites. The material does not perform well in reducing eddy current losses at these higher frequencies, limiting its use in high-frequency applications.
Efficiency:
Amorphous steel is highly efficient for low-frequency power applications because it has reduced core losses compared to traditional iron. However, for high-frequency use, its efficiency drops due to increased eddy current losses.
4. Powdered Iron
Material Characteristics:
Powdered iron is used in a variety of inductors and transformers. It is made of small iron particles bound together by an insulating material.
Performance at Different Frequencies:
Low Frequencies:
Powdered iron cores are suitable for low-frequency applications (50/60 Hz to a few kHz). The granular structure helps reduce eddy current losses, and the material provides good permeability and low loss at these frequencies.
High Frequencies:
At higher frequencies (above 100 kHz), powdered iron cores exhibit higher losses due to the increasing influence of eddy currents, though they may still perform better than solid iron cores at higher frequencies.
Efficiency:
Powdered iron offers good efficiency for medium-frequency applications (a few kHz to hundreds of kHz), but it becomes less efficient at higher frequencies due to higher core losses compared to ferrites.
5. Nanocrystalline Materials
Material Characteristics:
Nanocrystalline materials are a newer type of magnetic material that combines excellent soft magnetic properties with low core losses. These materials have a nanometer-scale crystalline structure.
Performance at Different Frequencies:
Low Frequencies:
Nanocrystalline cores perform well at low frequencies, offering low core losses, high saturation flux density, and high permeability, making them efficient for low-frequency power applications.
High Frequencies:
They also perform well at higher frequencies, from tens of kHz to several MHz, due to their low eddy current losses and reduced hysteresis losses.
Efficiency:
Nanocrystalline materials provide excellent efficiency across a wide range of frequencies, making them ideal for applications requiring low loss and high performance in both low and high-frequency ranges.
Summary of Core Material Performance:
If reading this on a mobile device ou may wish to rotate your display to facilitate the full width of the table
| Material | Frequency Range | Key Advantages | Key Disadvantages |
|---|---|---|---|
| Ferrites | High Frequencies (kHz to MHz) | Low eddy current losses, high permeability | Higher core losses at low frequencies |
| Iron (Laminate) | Low Frequencies (50/60 Hz) | High efficiency at low frequencies, reduced eddy currents | High eddy current losses at high frequencies |
| Amorphous Steel | Low Frequencies (50/60 Hz) | Low core losses, excellent for low-frequency power | Poor performance at high frequencies |
| Powdered Iron | Medium Frequencies (a few kHz to hundreds of kHz) | Reduced eddy current losses, good for mid-range frequencies | Higher core losses at higher frequencies |
| Nanocrystalline | Wide Range (Low to High Frequencies) | Low core losses across a wide frequency range | More expensive, limited availability |
Conclusion:
Low-frequency applications (like power transformers operating at 50/60 Hz)
benefit from iron cores, amorphous steel, and powdered iron due to their
low core losses and high saturation flux density.
High-frequency applications (like RF inductors or high-speed transformers)
favour ferrite and nanocrystalline materials, which offer low eddy current
losses and high permeability at these frequencies.
Efficiency is highly dependent on the core material's ability to minimize
core losses (hysteresis and eddy currents) and to provide adequate magnetic
permeability at the operating frequency.
By selecting the appropriate magnetic material based on the frequency range of operation, inductors and transformers can be optimized for maximum efficiency.
Recall that losses in the material will cause heating which affects power handling and the required physical size of the core for the power concerned.
Effects of Heating on Power Handling
Reduced Efficiency: As the core material heats up due to hysteresis and eddy current losses, the efficiency of the inductor or transformer decreases. More input energy is required to achieve the same output, leading to higher operational costs and reduced overall performance.
Thermal Runaway: If the core temperature rises too much, it can cause a phenomenon called thermal runaway, where the resistance of the core increases, leading to further heating and a vicious cycle of worsening efficiency. This could cause failure in the core or surrounding components.
Reduction in Power Handling: Core heating limits the amount of power the device can handle. Excessive heating can cause insulation breakdown, damaging the windings or the core itself, and limiting the maximum power that the device can transmit safely. If the losses are too high, the transformer or inductor may not be able to handle the required power without overheating.
Impact on Physical Size
Core Design and Size: To mitigate the losses and the associated heating, the core must often be designed larger, with better heat dissipation mechanisms (such as cooling fins or heat sinks) or higher quality core materials that have lower hysteresis and eddy current losses.
Material Selection: Core materials with lower losses at the operational frequency (e.g., amorphous steel or ferrites for high-frequency transformers) can reduce heating, allowing for a smaller core size.
Insulation and Cooling: The need to manage heat increases the physical size of the transformer or inductor. More insulation, cooling systems (such as oil immersion or forced air cooling), and thicker windings may be required, leading to an increase in the overall size and weight of the device.
Design Trade-Offs: Engineers must balance the need for a smaller core and lower losses with the physical limitations imposed by heating. Reducing core losses requires the use of higher-quality materials, but this can increase the cost and complexity of the design.
Conclusion
Heating caused by core material losses in inductors and transformers is a crucial factor that affects both power handling capacity and the required physical size of the device. Higher losses result in increased heating, reducing the efficiency, power handling, and longevity of the components. To address these challenges, careful attention must be paid to material selection, core design, and cooling mechanisms to optimize performance and manage heat dissipation effectively.
The origin of some of the text on this page is from the RSGB with additions by the web master