

2E6 Understand that impedance is a combination of resistance and reactance and apply the formula for impedance and current in a series CR or LR circuit.
The formulae are :- 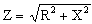

![]()
If there is a resistor and an inductor (and or a resistor and capacitor or even a resistor inductor and a capacitor) linked together in series in an AC circuit then the total opposition to the flow of current is known as impedance symbol Z.
Resistance and reactance CANNOT just be added together
Impedance is made up of both resistance R and reactance X, both are measured in ohms but cannot be added together ( as you can do for resistor in series ) but have to be added together like vectors :-
![]()
Ohms law can now be applied to the circuit and the current determined by the formula:-
![]()
Impedance as a Combination of Resistance and Reactance
Impedance (Z) is the total opposition to the flow of alternating current in a circuit. It is a complex quantity that combines both resistance (real part) and reactance (imaginary part).
Resistance (R) is the opposition to current due to the material's properties and does not change with frequency. Reactance (X) is the opposition to current caused by inductance or capacitance and is frequency-dependent:
Inductive Reactance ( XL ) increases with frequency.
Capacitive Reactance ( XC ) decreases with frequency.
R is the resistance in ohms (Ω).
In a series circuit, the impedance is the total opposition to current flow.
Impedance in a Series CR Circuit
In a series CR circuit (a capacitor and resistor in series), the impedance is the sum of the resistance R and the capacitive reactance XC. The capacitive reactance is given by:
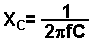
where: f is the frequency (Hz) of the AC signal, C is the capacitance (Farads).
In this case, the reactance is negative because a capacitor causes a phase shift where the current leads the voltage.
Impedance in a Series LR Circuit
In a series LR circuit (a resistor and inductor in series), the impedance is the sum of the resistance R and the inductive reactance XL. The inductive reactance is given by:
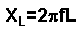
where: L is the inductance (Henrys) of the coil.
In this case, the reactance is positive because an inductor causes a phase shift where the voltage leads the current.
Magnitude of Impedance
In both cases, the impedance is a complex number. The magnitude of the impedance is given by:
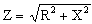
This represents the total opposition to current in the circuit, accounting for both resistance and reactance.
Current in the Circuit
Once the impedance Z is determined, the current I in the circuit can be found using Ohm’s Law for AC circuits:
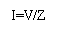
where:
V is the applied voltage (usually given in RMS form for AC)
Z is the impedance (in ohms).
Impedance is a complex number, the current I will also generally have both magnitude and phase.
Magnitude of Current:
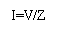
Phase of Current: The phase of the current will depend on the phase of the impedance, which is related to the phase of the voltage and the reactance.
Example: Series LR Circuit:
Given:
Calculate Inductive Reactance and Impedance:
XL = 2π x 50 x 0.5 =157.08Ω
Z = sq. root ( 102 + (1572) = 157.1 Ω
Current:
I = V/Z = 20 / 157.1 = 0.127 A
Series CR Circuit:
Given:
Calculate Capacitive Reactance and Impedance:
XC = 1 / (2π x 50 x 20 x 10-6) = 159.15 Ω
Z = sq. root ( 102 + (1592) = 157.1 Ω
Current:
I = V / Z = 20 / 157.1 = 0.127 A
By following the formulae in the above steps, you can calculate the impedance and current in both CR and LR circuits.
The origin of some of the text on this page is from the RSGB with additions by the web master